三次関数のグラフの書き方

三次関数のグラフの書き方を一から見ていきましょう。
三次関数のグラフを書くためには、グラフの極大値や極小値、変曲点といった箇所がどこにあるのかを調べ、
それらを表にまとめた増減表を書くことによって求めます。
それでは、三次関数のグラフの書き方について詳しく見ていきましょう。

• グラフを描画する裏技


• 三次関数の3タイプ
• 極大値・極小値について
• 極大値・極小値を求める
• 微分してグラフの傾きを表す関数を求める
• 傾きが0となる時の座標を求める
• 増減表を書く
• 追加情報を書き足す
• 実際にグラフを書いてみる


• 参考

本質からは外れてしまいますが、本サイトでは係数を入力するだけでグラフを自動的に描画するコンテンツも掲載しています。

手っ取り早く関数の形を知りたいという方は以下のリンクをクリックしてみてください。

係数を入力するだけで自動的にグラフを描画してくれるページ

学問に近道はありません。

三次関数のグラフの書き方がわからないという方は、自動描画ツールなんかに頼らず、このページでしっかりマスターしましょう。

三次関数の3タイプ

まず、三次関数のグラフが実際にどのような形をしているかを見ていきましょう。

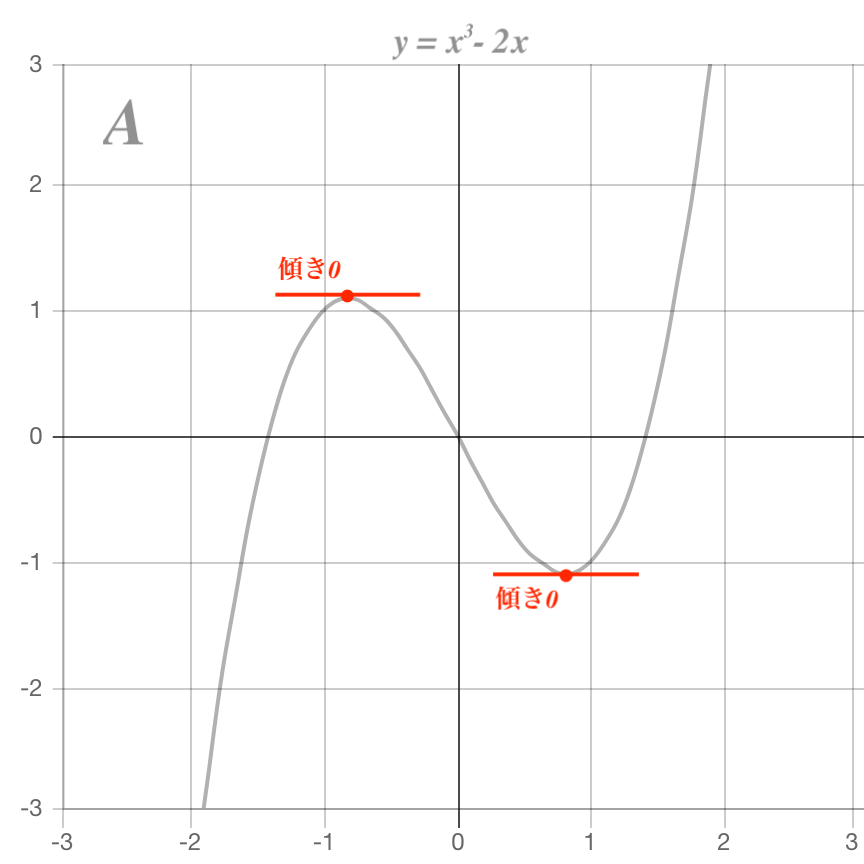
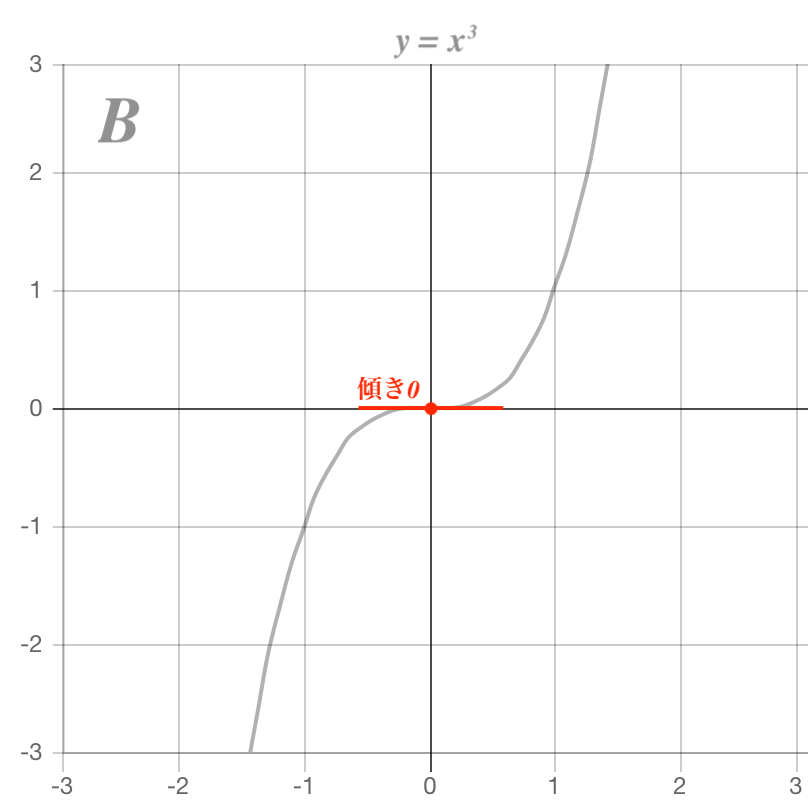
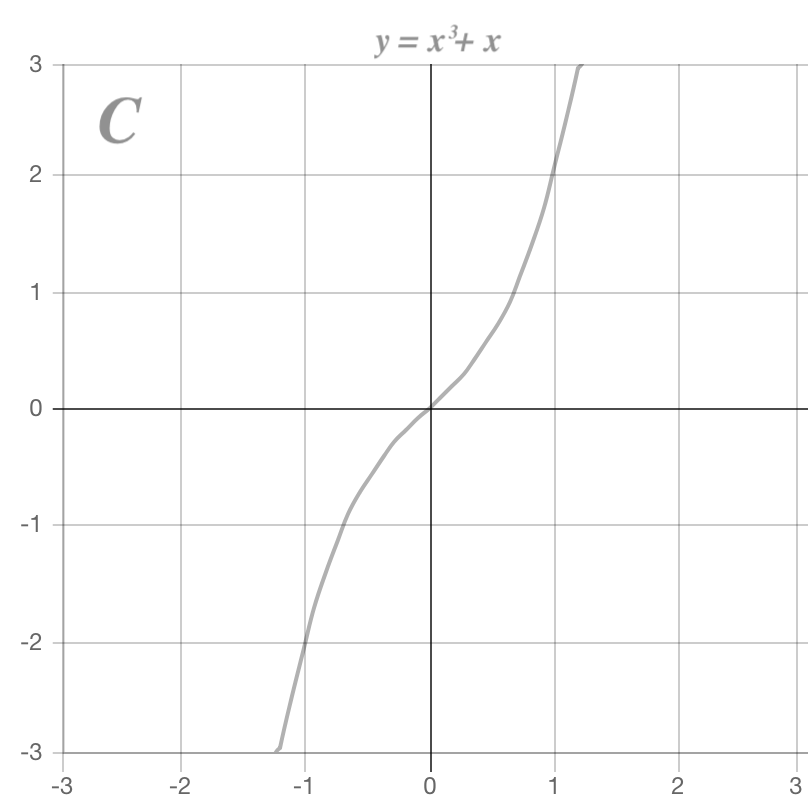
三次函数のグラフは上のグラフのような3種類に分類することができます。

A. 傾きが0となる点が2箇所ある
B. 傾きが0となる点が1箇所のみ
C. 傾きが0となる箇所が存在しない

極大値・極小値について

先ほどの3つのグラフのうち、Aのような傾きが0となる点が2箇所ある場合、その2箇所が極値をとります。（その周辺で値が最大または最小となる）

その周辺で値が最大となる場合、その値を極大値
その周辺で値が最小となる場合、その値を極小値

と呼びます。

また図中の青い点のように、グラフの曲がり具合が変わる点を変曲点と呼びます。

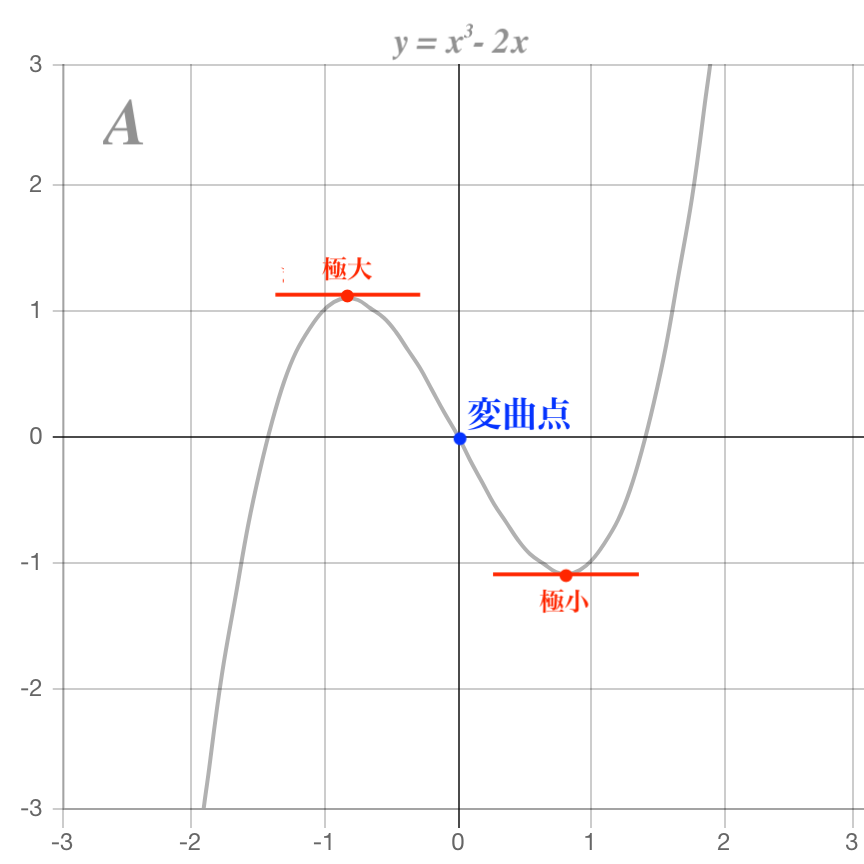
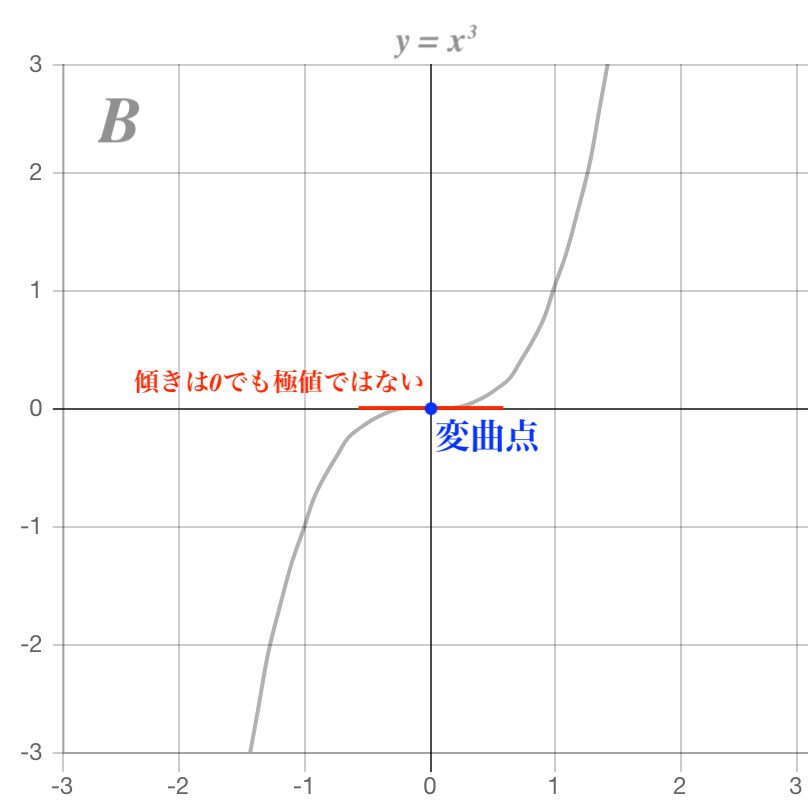
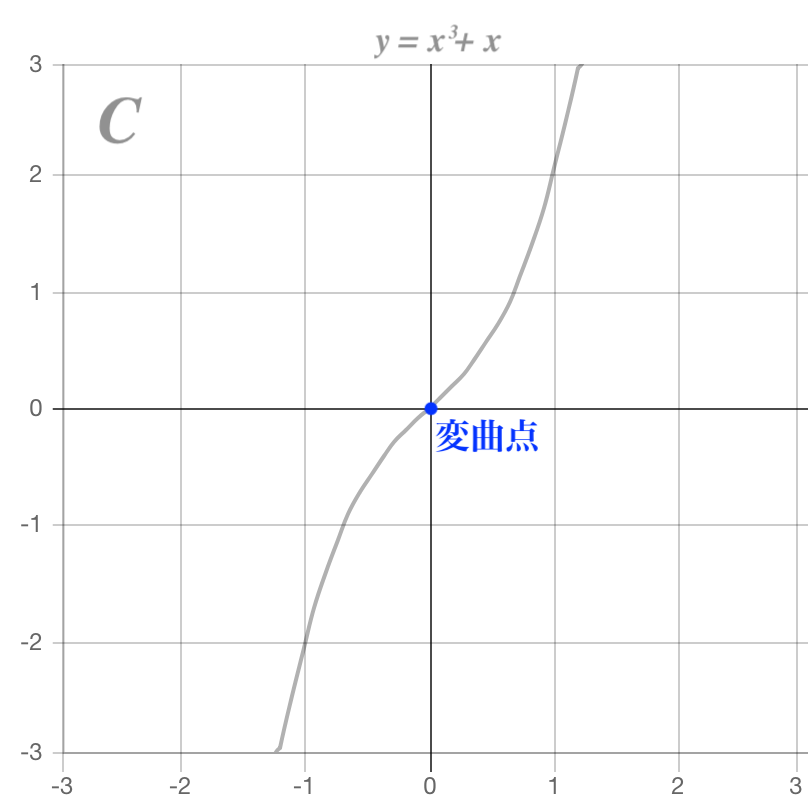
A. 傾きが0となる点が2箇所ある -> 極大値・極小値を持つ
B. 傾きが0となる点が1箇所のみ -> 極値を持たない（傾きが0でもその点は極値ではない）
C. 傾きが0となる箇所が存在しない -> 極値を持たない

極大値や極小値、変曲点の位置を求めることで、三次関数のグラフが書けるようになります。

check!

極大値・極小値を求める

早速、極大値・極小値を求めていきましょう。

極大値・極小値を求めるために、グラフの傾きが0となる点を探します。

関数を微分すると、微分後の関数は元の関数のグラフの傾きを表します。
例として、 y = x³ - 3x² - 9x + 2 のグラフの極大値・極小値を求めてみましょう。

check!

微分してグラフの傾きを表す関数を求める

y = x³ - 3x² - 9x + 2

    グラフの傾きを求めるために微分

y' = 3x² - 6x - 9

傾きが0となる時の座標を求める

先ほど求めたグラフの傾きを表す関数 = 0 として、傾きが0となる時の座標を求めよう。

3x² - 6x - 9 = 0
   
3 ( x² - 2x - 3 ) = 0
   
3 ( x - 3 ) ( x + 1 ) = 0

よって、傾きが0となる時のx座標は -1, 3 となる。

y座標も求めると、元の関数 y = x³ - 3x² - 9x + 2に x = -1, x = 3 をそれぞれ代入して、

( -1, 7 ) , ( 3, 25 ) を通ることがわかる。

今回はy' = 0の解を求めた時に解が2つ出てきたので、上の方に出てきたグラフのパターンA(傾きが0となる箇所が2つあり、極大値・極小値を持つ）に当てはまるわけだ。

y' = 0の式変形の結果が、( x - a )² = 0のような重解の形となる場合はパターンB、

y' = 0の式変形の結果が、解なし（二次関数の解の公式でルートの中がマイナスとなるような場合）になる場合はパターンCとなる。

check!

増減表を書く

次に、今までの計算結果を表にまとめた増減表を書きます。

まず、わかっている情報で表を作ります。
表は上から順番にx, y', yとします。

x = -1, x = 3 の時に極値を持つことがわかったので、この2つの値を表に記します。
すると下のような表が出来上がります。

x	...	-1	...	3	...
y'		0		0
y		7		-25

追加情報を書き足す

x = -1, x = 3の時にどこを通るかはわかりましたが、それ以外の時はどうなっているでしょうか。

仮にx = -2の時を調べてみましょう。
この時のグラフの傾きは、y'の式に代入すると15となります。この時のy'の符号が重要となります。

x = -2の時、y'の符号が正であるためこの区間ではグラフの傾きが正 = グラフが右上がりであることがわかります。
これも増減表に書き記します。

y'の符号が負の場合にはグラフの傾きが負 = グラフが右下がりとなります。

x	...	-1	...	3	...
y'	+	0		0
y	↗️	7		-25

同様にして、その区間で適当な1点を調べてその時の符号を調べ、増減表を完成させましょう。

x	...	-1	...	3	...
y'	+	0	-	0	+
y	↗️	7	↘️	-25	↗️

check!

実際にグラフを書いてみる

先ほど書いた増減表を元に、いよいよグラフを書いていきます。
まず、グラフがどの点を通るかを記します。

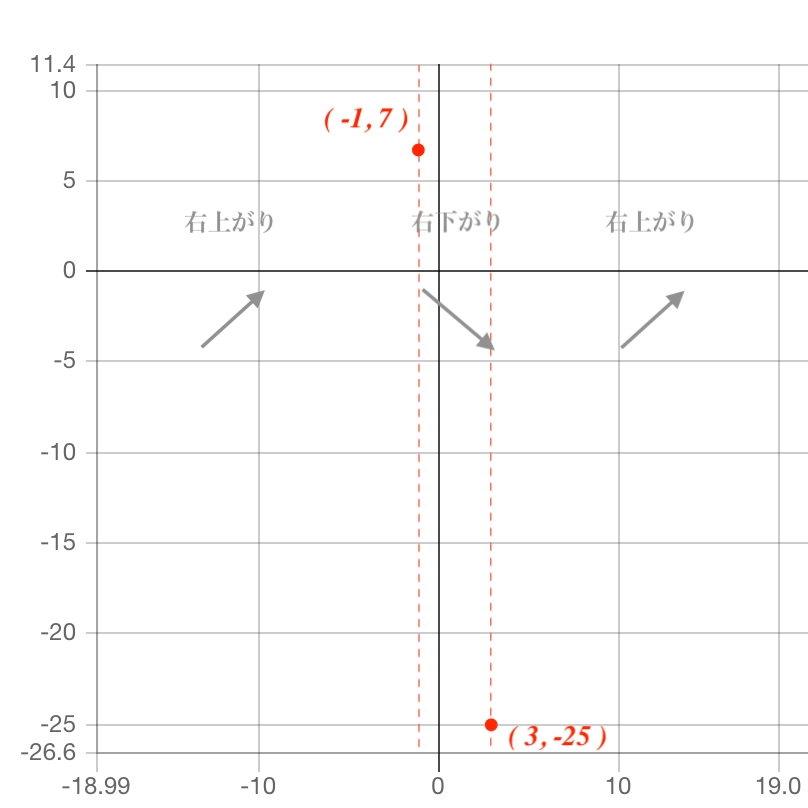
右上がり・右下がりの情報を元に、この2点を滑らかに繋ぎます。

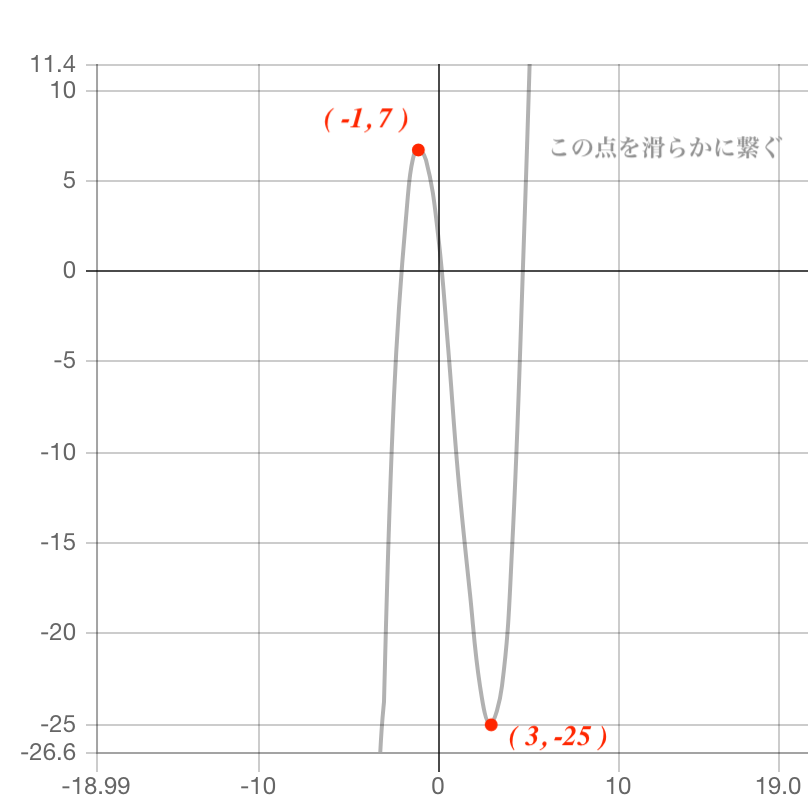
上手く書けましたか？
これで三次関数のグラフの書き方はマスターできましたね。

参考

正しく書けたかどうか不安な方は、こちらのページを利用して確認してみても良いでしょう。

係数を入力するだけで自動的にグラフを描画してくれるページ